|
|
|
1.
|
Solve 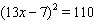 .
|
|
|
2.
|
Solve 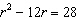 by factoring. a. | 14 and –2 | c. | 14 and 13 | b. | 13 and –2 | d. | 13 and –1 |
|
|
|
3.
|
Find the zeros of the function 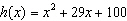 .
|
|
|
4.
|
Find the square root of the number 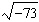 .
|
|
|
5.
|
Add. Write the result in the form 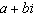 . (7 – 9 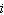 ) + (–6 + 5 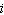 ) a. | 12 – 15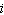 | c. | –2 – 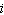 | b. | 1 – 4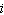 | d. | 13 – 14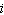 |
|
|
|
6.
|
What is the product 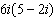 in the form 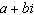 ?
|
|
|
7.
|
Solve 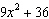 = 0.
|
|
|
8.
|
What value of d makes the equation 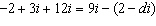 true?
|
|
|
9.
|
Complete the square for 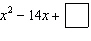 . Then write the resulting
expression as the square of a binomial.
|
|
|
10.
|
Solve by completing the square. 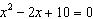
|
|
|
11.
|
Write the quadratic function 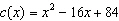 in vertex form.
|
|
|
12.
|
Solve 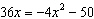 .
|
|
|
13.
|
Use the Quadratic Formula to solve 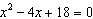 .
|
|
|
14.
|
Use the discriminant to find the number and type of solutions for 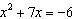 . a. | The equation has one real solution. | b. | The equation has two real
solutions. | c. | The equation has two nonreal complex solutions. | d. | Cannot determine
without graphing. |
|
|
|
15.
|
Solve the equation 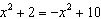 using a graph.
|
|
|
16.
|
Solve the system formed by the equations below. 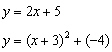
|
|
|
17.
|
The function 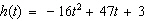 gives the height h, in feet, of a
football as a function of time t, in seconds, after it is kicked. Rewrite the function by
factoring. How long does it take for the football to hit the ground?
|
|
|
18.
|
A catapult set atop a hill overlooking an enemy castle fires a boulder at that
castle. The equation that represents the height 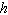 in feet of the boulder
above the ground the castle is built on is 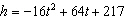 , where 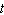
is the time in seconds after the boulder is launched. a. Rewrite the equation in the form 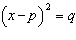 for the case where a boulder strikes the castle wall 25 feet above the
ground. b. How long is the boulder in part a in the
air?
|
|
|
19.
|
Part A: Solve the system formed by the equations below. Round to
the nearest hundredth if necessary. Describe the graph of this system. 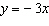 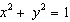 Part B: Part B: Is it possible for a system like the one above to have exactly
one solution? Explain why or why not.
|
|
|
20.
|
A punter kicks a football 4 feet above the ground with an initial upward
velocity of 64 feet per second. a.
The height above the ground in feet of an object h with an initial upward velocity in feet per
second 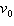 and an initial height in feet 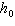 is 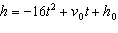 , where 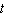 is the time
in seconds. Write an equation for the height of the football after 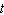
seconds. b. Write an inequality that represents the time when the
football is at least 52 feet high. c. At what times after the ball
is kicked is the football at least 52 feet high?
|