|
|
|
1.
|
Compare the graph of 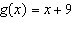 with the graph of 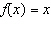 .
|
|
|
2.
|
Compare the graph of 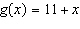 with the graph of 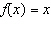 .
|
|
|
3.
|
Compare the graph of 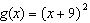 with the graph of 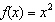 . a. | The graph of g(x) is translated 9 units left from the graph of
f(x). | b. | The graph of g(x) is translated 9
units right from the graph of f(x). | c. | The graph of g(x) is translated 9
units up from the graph of f(x). | d. | The graph of g(x) is translated 9
units down from the graph of f(x). |
|
|
|
4.
|
Compare and contrast the graphs of f( x) = x and
g( x) = 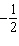 x x.
|
|
|
5.
|
a. | 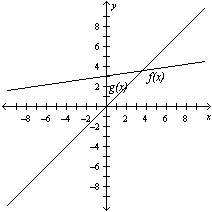
The transformations are a shrink and a
translation. | c. | 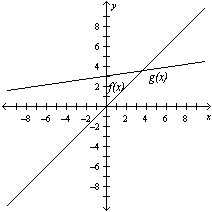
The transformations are a translation, a
reflection, and a shrink. | b. | 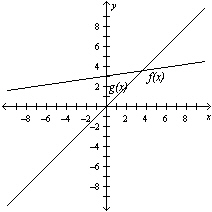
The transformations
are a shrink and a reflection. | d. | 
The transformations are a translation and
a reflection. |
|
|
|
6.
|
Describe the transformations applied to the graph of the parent function  used to graph  .
|
|
|
7.
|
Let  be a vertical shift of 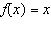
up 4 units followed by a vertical stretch by a factor of 3. Write the rule for 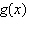 .
|
|
|
8.
|
Write a function that transforms 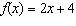 in the following
way: vertical stretch by a factor of 6 and shift 5 units left.
|
|
|
9.
|
What are the y-intercepts of the graphs of the functions? Equation
A  Equation B 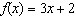
|
|
|
10.
|
Which function models the relationship between 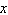 and 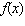 shown in the table?
|
|
|
11.
|
Rita reads a book at a steady pace. Rita graphs her progress through the book by
putting the time in hours 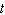 on the horizontal axis and chapters remaining
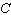 on the vertical axis. Which equation
describes Rita’s graph? 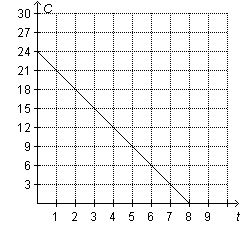
|
|
|
12.
|
Decide which linear function is increasing at a greater rate. Explain your
answer. --Linear Function 1 has an x-intercept of –2 and a y-intercept of
1. --Linear Function 2 includes the points in the table.
|
|
|
13.
|
Decide which linear function is increasing at a greater rate. Graph of
Linear Function 1: has an 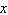 -intercept of 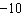 and a
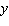 -intercept of 5. Graph of Linear
Function 2: passes through the points in the table below. 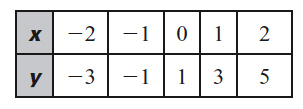
|
|
|
14.
|
Leah pays $40 a month for cable TV, plus $4 for each movie she orders on
pay-per-view. Which equation gives Leah’s total monthly cable bill as a function of the number
of pay-per-view movies m that she orders?
|
|
|
15.
|
The cost of a school banquet is $95 plus $15 for each person attending. Write an
equation that gives total cost as a function of the number of people attending. What is the cost for
77 people?
a. | y = 15x – 95; $1060 | c. | y = 15x + 95;
$1250 | b. | y = 95x + 15; $7330 | d. | y = 95x – 15;
$7300 |
|
|
|
16.
|
Lucy pays $211 in advance on her account at the athletic club. Each time she
uses the club, $5 is deducted from the account. Write a linear function that gives the value
remaining in her account after x visits to the club. Find the value remaining in the account
after 10 visits.
|
|
|
17.
|
Which equation best fits the data?
|
|
|
18.
|
The table shows the number of minutes per day that members of a cross-country
team spent practicing over the summer and the members’ mile times the following
semester. | Daily
practice (min) | 0 | 30 | 20 | 0 | 15 | | Mile time (min) | 8.5 | 5.5 | 6.5 | 6.5 | 7 | | | | | | |
Which equation
represents a line of best fit for these data?
|
|
|
19.
|
Given the following system of equations, what number should you multiply the
first equation by so that the x-term will be eliminated when the first equation is added to
the second equation? 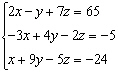
|
|
|
20.
|
Solve 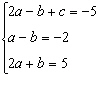 by substitution.
|