|
|
|
1.
|
Graph the quadratic function f(x) =
–5x2.
|
|
|
2.
|
Graph the quadratic function f(x) =
–3.75x2 + 2.
|
|
|
3.
|
Find the axis of symmetry and the vertex of the graph of f(x) =
3x2 – 6x – 1.
|
|
|
4.
|
Graph the quadratic function f(x) = 2x2 +
4x – 2.
|
|
|
5.
|
Graph the quadratic function 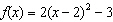 .
|
|
|
6.
|
Graph the quadratic function f(x) = (x + 3)(x +
2).
|
|
|
7.
|
The graph shows the height  of a model rocket  seconds after it is launched from the ground at 112 feet per second. Where is the height
of the rocket increasing? Where is it decreasing? 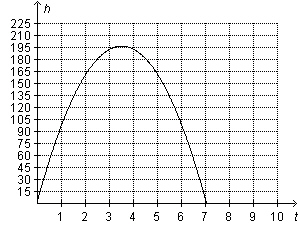 a. | The height of the rocket is always increasing. | b. | The height of the
rocket is always decreasing. | c. | The height of the rocket is increasing when
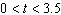 and decreasing when and decreasing when 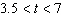 . . | d. | The height of the rocket is increasing when 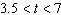 and
decreasing when and
decreasing when 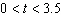 . . |
|
|
|
8.
|
Use the given information to decide which quadratic function has the lesser
minimum value. Quadratic Function 1 whose equation is 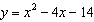 or Quadratic Function 2
whose graph is shown below.
|
|
|
9.
|
How would you translate the graph of 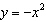 to produce the graph of
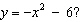 a. | translate the graph of 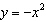 right 6 units right 6 units | b. | translate the graph
of 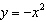 up 6 units up 6 units | c. | translate the graph
of 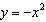 left 6 units left 6 units | d. | translate the graph
of 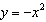 down 6 units down 6 units |
|
|
|
10.
|
Use this description to write the quadratic function in vertex form: The
parent function 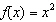 is vertically compressed by a factor of 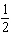 and translated 11 units left and 5 units down.
|
|
|
11.
|
Write the function 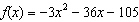 in vertex form, and identify its
vertex. a. | 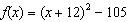 ; ;
vertex: (–12,
–105) | c. | 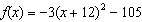 ; ;
vertex: (–12,
–105) | b. | 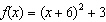 ; ;
vertex: (–6, 3) | d. | 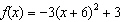 ; ;
vertex: (–6,
3) |
|
|
|
12.
|
Find the maximum value of each quadratic function. Then decide which function
has the greater maximum value. --Quadratic Function 1: The function whose equation is 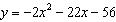 . --Quadratic Function 2: The function whose graph is shown. 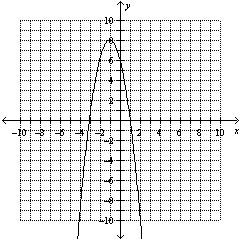 a. | The maximum value of Quadratic Function 1 is –5.5.
The maximum value of
Quadratic Function 2 is –1.
Quadratic Function 2 has the greater maximum
value.
| b. | The maximum value of Quadratic Function 1 is –5.5.
The maximum value of
Quadratic Function 2 is 8.
Quadratic Function 2 has the greater maximum
value.
| c. | The maximum value of Quadratic Function 1 is 4.5.
The maximum value of Quadratic
Function 2 is 8.
Quadratic Function 2 has the greater maximum value.
| d. | The maximum value of
Quadratic Function 1 is 4.5.
The maximum value of Quadratic Function 2 is –1.
Quadratic
Function 1 has the greater maximum value.
|
|
|
|
13.
|
Two identical rubber balls are dropped from different heights. Ball 1 is dropped
from a height of 16 feet, and the ball 2 is dropped from a height of 64 feet. Write and graph a
function for the height of each ball. Then use the graphs to tell when each ball will reach the
ground.
|
|
|
14.
|
Find the zeros of the function 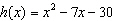 .
|
|
|
15.
|
The table gives the number of inner tubes, I, sold in a bike shop between
2009 and 2014. Determine which model best fits the data. Year, t | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | Inner tubes, I | 16 | 37 | 66 | 129 | 259 | 516 | | | | | | | |
a. | absolute value | b. | exponential | c. | quadratic | d. | linear |
|
|
|
16.
|
The graph shows the distance, d, a car is traveling over time, t.
What is the average rate of change between points P and Q? 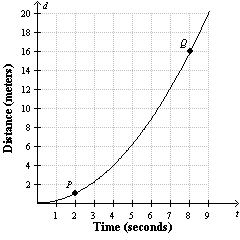
|
|
|
17.
|
Examine the two graphs of the same four functions. Which function has the
greatest function values as x gets larger and larger? 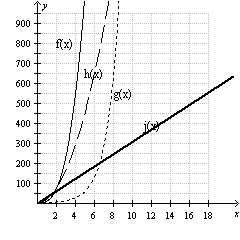 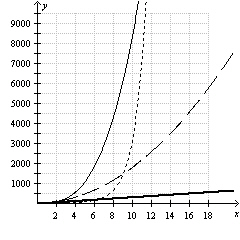
|
|
|
18.
|
Which function has greater function values as x gets larger and larger?
Use a table or graph to identify the function.
|
|
|
19.
|
A golf ball is hit from a tee on the ground. The golf ball reaches
a maximum height of 20 meters and travels a horizontal distance of 117 meters.
Part
A: What type of function should you use to represent the path of the golf ball?
Explain.
Part B: In the context of the given situation, what do the
intercepts and maximum point represent?
|
|
|
20.
|
A student is looking for a quadratic function that fits the points (–5,
80), (0, –5), and (7, 128). He incorrectly believes f( x) = 3 x2
+ 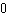 x x – 5 is the solution, based on
his work below. Explain where the student made his first error and what he should have done
differently at that point. What is the correct function?
(x, y) | f(x) = ax2 + bx +
c | (–5, 80) | 80 =
a(–5)2 + b(–5) + c | (0, –5) | –5 = a(0)2 + b(0) +
c | (7, 128) | 128 =
a(7)2 + b(7) + c | | |
Because c = –5 ,
80 =
a(–5) 2 + b(–5) – 5
128 = a(7) 2 +
b(7) – 5 can be rewritten as 25 a – 5 b = 85 49 a +
7 b = 133 This system can be solved by linear combination. | 175a – 35b = 595 | | 245a + 35b =
665 | |
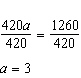 Substituting one of the ordered pairs gives 80 = 3(–5) 2
+ b(–5) – 5 80 = 75 – 5 b – 5 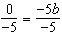 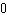 = b
and the function is
f( x) = 3 x2 + 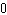 x x – 5.
|