Name: 
 

Algebra 1 Chapter 6 Practice Test


 1. 
How could you write 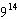mc001-1.jpgas a product of powers?
a.
A power with a base of 81 and 196 as the exponent.
b.
Multiply two powers, both with a base of 9. The product of the exponents should be 14.
c.
Multiply two powers, both with exponents of 14. The product of the bases should be 9.
d.
Multiply two powers, both with a base of 9. The sum of the exponents should be 14.
 

 2. 
Evaluate mc002-1.jpg for mc002-2.jpg and mc002-3.jpg.
a.
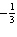mc002-4.jpg
c.
0
b.
3
d.
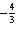mc002-5.jpg
 

 3. 
Simplify: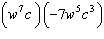
mc003-1.jpg
a.
mc003-2.jpg
c.
mc003-4.jpg
b.
mc003-3.jpg
d.
mc003-5.jpg
 

 4. 
Write the expression 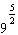mc004-1.jpg in radical form, and then evaluate. Round to the nearest whole number if necessary.
a.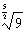
mc004-2.jpg; 243
c.
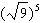mc004-4.jpg; 243
b.
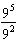mc004-3.jpg; 729
d.
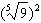mc004-5.jpg; 2
 

 5. 
Simplify the expression 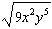mc005-1.jpg. All variables represent nonnegative numbers.
a.
mc005-2.jpg
c.
mc005-4.jpg
b.
mc005-3.jpg
d.
mc005-5.jpg
 

 6. 
The surface area S of a cube with volume V is 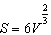mc006-1.jpg. What effect does increasing the volume of the cube by a factor of 2 have on the surface area?
a.
The surface area increases by a factor of mc006-2.jpg.
b.
The surface area increases by a factor of 2.
c.
The surface area increases by a factor of 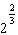mc006-3.jpg.
d.
The surface area increases by a factor of 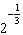mc006-4.jpg.
 

 7. 
How does the function represented in the table change over equal intervals? What does this tell you about the type of function it is?

x
8
18
28
38
f(x)
4
8
16
32
a.
The function does not change by equal factors over equal intervals. The function is a not an exponential function.
b.
The function changes by equal differences over equal intervals. The function is an exponential function.
c.
The function changes by equal factors over equal intervals. The function is an exponential function.
d.
The function does not change by equal factors over equal intervals. The function is an exponential function.
 

 8. 
Which statements are true about the graph of the exponential function 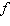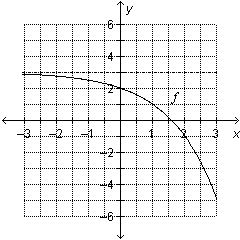mr008-1.jpg?

mr008-2.jpg
 a.
The domain is all real numbers.
 b.
The range is all real numbers.
 c.
The mr008-19.jpg-intercept is 2.
 d.
The mr008-20.jpg-intercept is 2.
 e.
As mr008-21.jpg increases without bound, mr008-22.jpg decreases without bound.
 f.
As mr008-23.jpg decreases without bound, mr008-24.jpg approaches, but never reaches, mr008-25.jpg.
 

 9. 
In the year 2000, the population of Mexico was about 100 million, and  was growing by approximately 1.53% per year. At this growth rate, the function 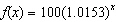mc009-1.jpg gives the population, in millions, x years after 2000. Using this model and a graph of the function, in what year would the population reach 111 million? Round your answer to the nearest year.
a.
2006
c.
2007
b.
2005
d.
2008
 

 10. 
If there are initially 4500 bacteria in a culture, and the number of bacteria doubles each hour, the number N of bacteria after t hours can be found using the formula 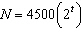mc010-1.jpg. About how long will it take the culture to grow to 80,000 bacteria?
a.
37.75 hr
b.
2.5 hr
c.
1.25 hr
d.
4.15 hr
 

 11. 
The population of a town is currently 1928 people and is expected to triple every 4 years. How many people will be living there in 20 years?
a.
156,168
c.
38,560
b.
13,947,137,604
d.
468,504
 

 12. 
A radioactive isotope decays exponentially. The time it takes for half of the amount to decay is called the isotope’s half-life. A certain isotope has a half-life of 8 hours. If after 24 hours there are 0.981 mg left, what was the isotope’s initial mass?
a.
7.848 mg
c.
31.392 mg
b.
0.327 mg
d.
251.136 mg
 

 13. 
Write an exponential function to model a population of 240 animals that decreases at an annual rate of 14%. Then estimate the value of the function after 5 years (to the nearest whole number).
 

 14. 
Solve 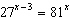mc014-1.jpg.
a.
x = –9
c.
x = –10
b.
x = 10
d.
x = 9
 

 15. 
Which graph demonstrates that the equation 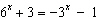mc015-1.jpg has no solution?
a.
mc015-2.jpg
c.
mc015-4.jpg
b.
mc015-3.jpg
d.
mc015-5.jpg
 

 16. 
Find the first 4 terms of the geometric sequence for which 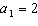sa016-1.jpg and 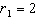sa016-2.jpg.
 

 17. 
What is the 18th term in the following geometric sequence?

4, 8, 16, 32, 64, ...
a.
1,048,576
c.
524,288
b.
131,072
d.
–524,288
 

 18. 
Find the first 5 terms of the sequence with 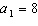mc018-1.jpg and 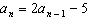mc018-2.jpg.
a.
8, 16, 32, 64, 128
c.
8, 11, 17, 29, 53
b.
1, 2, 3, 4, 5
d.
8, 9, 10, 11, 12
 

 19. 
Write a recursive rule for the sequence.
–5, –10, –20, –40, . . .
a.
mc019-1.jpg; mc019-2.jpg
c.
mc019-5.jpg; mc019-6.jpg
b.
mc019-3.jpg; mc019-4.jpg
d.
mc019-7.jpg; mc019-8.jpg
 

 20. 
Write a recursive rule for the sequence.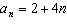
mc020-1.jpg
a.
mc020-2.jpg
c.
mc020-4.jpg
b.
mc020-3.jpg
d.
mc020-5.jpg
 

 21. 
Write an explicit rule for the sequence.
a1 = –9, an = 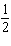mc021-1.jpgan – 1
a.
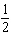an = –9(mc021-2.jpg)n – 1
c.
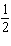an = –(mc021-3.jpg)n – 1
b.
an = (–9)n – 1
d.
an = (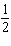mc021-4.jpg)(–9)n – 1
 

 22. 
You are depositing $50 each month in a credit union savings club account. You are getting 0.7% monthly (8.4% annually) interest on the account. The balance at the beginning of the nth month can be given by the following recursive function.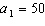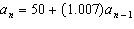
mc022-1.jpg
mc022-2.jpg
Find the balance at the beginning of the 6th month.
a.
$302.10
c.
$305.29
b.
$306.29
d.
$303.52
 

 23. 
The table displays the speed of a car pr023-1.jpg, in feet per second, pr023-2.jpg seconds after it starts coasting.

Time, 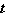pr023-3.jpg
(seconds)
Speed, 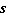pr023-4.jpg
(ft/sec)
1
57
2
54.15
3
51.44
4
48.87

a.      Explain why this sequence is geometric.
b.      Write an explicit rule for this sequence using the values from the table.
c.      Use the result from part (b) to write a recursive rule for this sequence.
d.      What is the speed of the car when it begins to coast?
 



 
Check Your Work     Start Over